1. Derivative Of Arctan 1
2. Derivative Of Arctan(3x)

Find the first derivative of f(x) = arctan x + x 2 Solution to Example 2: Let g(x) = arctan x and h(x) = x 2, function f may be considered as the sum of functions g and h: f(x) = g(x) + h(x). Hence we use the sum rule, f '(x) = g '(x) + h '(x), to differentiate function f as follows f '(x) = 1 / (1 + x 2 ) + 2x = (2x 3 + 2x + 1) / (1 + x 2 ).

DERIVATIVES OF INVERSE TRIGONOMETRIC FUNCTIONS

• Assuming we know the derivative of tan(x) is sec 2 (x): Let y = arctan(x) so that x = tan(y). Differentiate both sides with respect to x to get: 1 = sec 2 (y) dy/dx. Now use the identity. Sin 2 (y) + cos 2 (y) = 1. Divide by cos 2 (y) to get. Tan 2 (y) + 1 = sec 2 (y) Use the substitution tan(y) = x to get. Sec 2 (y) = 1 + x 2.
• Free derivative calculator - differentiate functions with all the steps. Type in any function derivative to get the solution, steps and graph.

Differentiation of inverse trigonometric functions is a small and specialized topic. However, these particular derivatives are interesting to us for two reasons. First, computation of these derivatives provides a good workout in the use of the chain rule, the definition of inverse functions, and some basic trigonometry. Second, it turns out that the derivatives of the inverse trigonometric functions are actually algebraic functions!! This is an unexpected and interesting connection between two seemingly very different classes of functions.

It is possible to form inverse functions for restricted versions of all six basic trigonometric functions. One can construct and use an inverse cosecant function, for example. However, it is generally enought to consider the inverse sine and the inverse tangent functions. We will restrict our attention to these two functions.

Here are the results.

Derivatives of Inverse Trigonometric Functions

d dx arcsin(x) = 1 sqrt(1-x2)

d dx arctan(x) = 1 x2+1

y = arcsin(x)
-1 x 1

The arctangent function is differentiable on the entire real line. The arcsine function is differentiable only on the open interval (-1,1). Even though both 1 and -1 are in the domain of the arcsine function, the arcsine is not differentiable at these points. From an algebraic point of view, we see that neither 1 nor -1 can be plugged into the derivative formula for arcsine...there's that thing about never dividing by zero again!! From a graphical point of view, the graph of the arcsine function has vertical tangent lines at the endpoints (1,/2) and (-1,-/2).

In order to verify the differentiation formula for the arcsine function, let us set

y = arcsin(x).

We want to compute dy/dx. The first step is to use the fact that the arcsine function is the inverse of the sine function. Among other things, this means that

sin(y) = sin(arcsin(x)) = x.

Next, differentiate both ends of this formula. We apply the chain rule to the left end, remembering that the derivative of the sine function is the cosine function and that y is a differentiable function of x.

d dx sin(y)	=	d dx x
cos(y) dy dx	=	1

The next step is to solve for dy/dx. (After all, this is the thing that we want to compute!)

dy dx

=

1 cos(y)

=

sec(y)

This looks like progress, but it is not the answer. Remember, when we differentiate a function of x in terms of x (this is the meaning of the dx in d/dx), we must express our answer in terms of x. Therefore the question remains.

If sin(y)=x, what is cos(y) in terms of x?

sin(y) = x

The key is to construct a 'reference triangle' to record the relationship between x and y. This is a right triangle with the angle y (measured in radians) as one of the acute angles. The trigonometric functions of y can then be expressed as ratios of side lengths in this triangle. Note that we built our triangle in such a way that the side opposite to y has length x and so that the hypotenuse has length 1. This provides thatsin(y) = opposite/hypotenuse = x/1 = x.
The length of the third side of the reference triangle is determined by the Pythagorean Theorem.

1²=x²+(third side)²
(third side)² = 1-x²
third side=sqrt(1-x²)

The last step is to express the trigonometric functions of y in terms of ratios of side lengths in the reference triangle. In particular, the secant of y is equal to the hypotenuse length divided by the adjacent side length.

d dx arcsin(x)

=

dy dx

=

sec(y)

=

1 sqrt(1-x2)

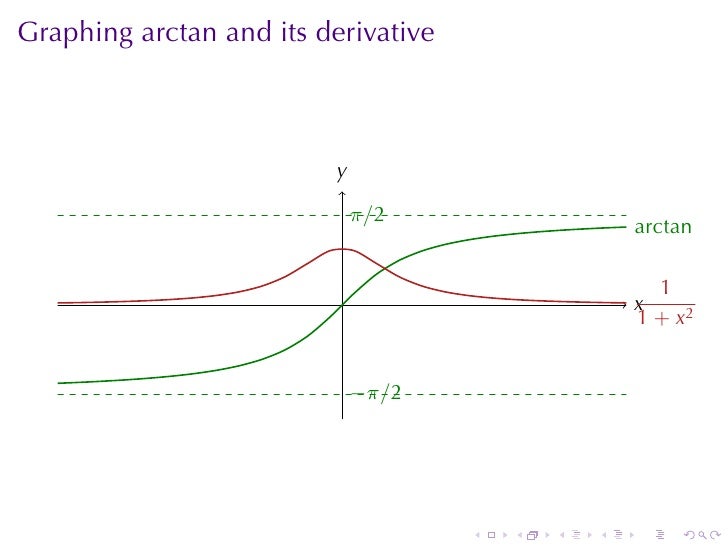
Derivative Of Arctan 1

tan(y) = x

Verification of the derivative formula for the arctangent function is left as an exercise.....an exercise that is highly recommended!! The procedure is the same as the one that we used above. Begin by setting y=arctan(x) so that tan(y)=x. Differentiating both sides of this equation and applying the chain rule, one can solve for dy/dx in terms of y. One wants to compute dy/dx in terms of x. A reference triangle is constructed as shown, and this can be used to complete the expression of the derivative of arctan(x) in terms of x.

This completes our study of differentiation for now. In Stage 6, we will investigate another general differentiation technique called implicit differentiation. Later still, we will learn how to differentiate exponential and logarithmic functions. For now, you should go to the Practice area and spend some time learning to use the many differentiation techniques that have been introduced in this Lesson. If there is one skill that we must develop for success in differential calculus, it is differentiation!! Enjoy, and good luck!!

If you find that you are having difficulty with differentiation, don't worry. You're not the first person to struggle with this technical skill. Contact your classmates. Discuss your difficulties. Contact your instructor. We can learn to do this!!

We now turn to the exponential and logarithmic functions. We have already discussed 'the' exponential function: exp(x)=e^x. In order to differentiate the 'other' exponential functions and the logarithmic functions, we must first compute the derivative of the inverse to the exponential function. Thus we turn our attention to the natural logarithm.

/Stage6/Lesson/invTrigDeriv.html

COVER

CQ DIRECTORY

HUB

CQ RESOURCES

© CalculusQuest^TM
Version 1
All rights reserved---1996
William A. Bogley
Robby Robson

What is the derivative of #y=arctan(cos(x))#?

1 Answer

This is a case of knowing the how the derivative of inverse tangent works, and then following the chain rule.

If we were looking at #y=arctan(x)#, there's a way to determine the derivative if you've forgotten the formula.

First remember that #arctan(x)# means 'inverse tangent of x,' sometimes written as #tan^(-1)(x)#. To invert means to switch the x and the y (among other things, but that's the important meaning here).

So #y=tan^(-1)(x)# means the same thing as

#x=tan(y)#

Notice the tangent is no longer an inverse after the switch.

Now we can use implicit differentiation. That's where we don't care whether or not we're looking at a function, that is, we don't care if we have y on one side and everything else on the other. We just derive everything as we go along, and we write #dy/dx# after every term that contains a y (that's a very, very over-simplified explanation of implicit differentiation, but it will work for this problem).

So we derive

#x=tan(y)#

and we get

#1=sec^2(y) dy/dx#

which is the same as

#dy/dx=cos^2(y)#

Which seems straightforward enough. Except for one thing. We don't usually have derivatives that still have y's in them. Not in the first year of Calculus, anyway. We should get rid of that y.

We can go back to a right triangle here. We started with #x=tan(y)#. Than means that there is a right triangle somewhere where the angle is y and the tangent of that angle is x, or #x/1#.

So:

Then by the Pythagorean Theorem, the hypotenuse can be found:

#a^2+b^2=c^2#

#1^2+x^2=c^2#

#c=sqrt(1+x^2)#

So the #cos(y)=1/sqrt(1+x^2)#

meaning that if

#y=tan^(-1)(x)#

then

#dy/dx=cos^2(y)#

which is the same as

#dy/dx=1/(1+x^2)#

So if we're looking at #y=arctan(cos(x))#, then we apply the derivative rule above, with the chain rule.

Derivative Of Arctan(3x)

The chain rule say that if you have an 'inside function' and an 'outside function,' then you take the derivative of the outside function, and multiply that by the derivative of the inside function, or

If #y=f(g(x))#

#dy/dx=f'(g(x))g'(x)#

Notice the inside function does not change when you derive the outside function.

If #y=arctan(cos(x))#, then my outside function is #y=arctan(x)# (and now we know that derivative). My inside function is #cos(x)#.

Finally:

#y=arctan(cos(x))#

#dy/dx=1/(sqrt(1+(cos(x)^2))) (-sin(x))#

since the derivative of #cos(x)# is #-sin(x)#.

Written more simply,

#dy/dx= (-sin(x))/(sqrt(1+cos^2(x)))#

Hope this helps.

Related topic

Related questions